Gracias a Nito, obtuve parte del examen de TALF de la convocatoria ordinaria de junio de 2009. Os lo muestro a continuación, mañana pondré las soluciones para compartirlas con vosotros.
Ejercicio común:
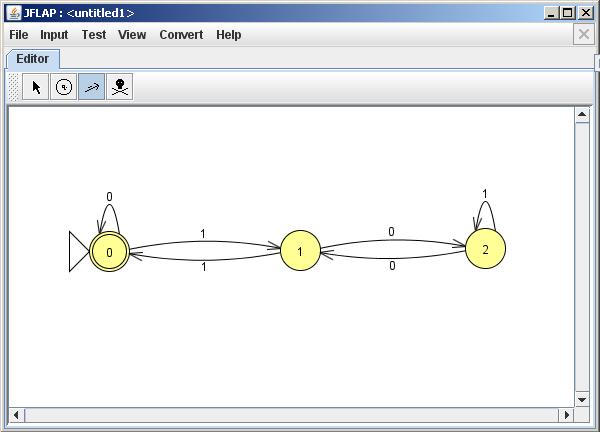
- Construir una gramática lineal por la derecha que genera todas las cadenas de bits w(es decir, w Є{0,1}*) que son divisibles sin resto por 3 (se interpreta w como número binario).
El lenguaje aceptado por el autómata sería L = { w | w Є {0,1}* w mod 3 = 0}
w en base 10 …. w en base 2 ………….. mod 3
0 ………………………. 0 …………………. 0
1 ………………………. 1 …………………. 1
2 ………………………. 10…………………. 2
*3 …………………….. 11 …………………. 0
4 ………………………. 100 ……………… 1
5 ………………………. 101 ……………….. 2
*6 …………………….. 110 …………………0
7 ………………………. 111 ………………..1
8 ………………………. 1000 ………………2
*9 …………………….. 1001 ……………… 0
.
.
.
Nº estados del autómata = nº de restos = 3 (estados 0, 1 y 2)
Preguntas de teoría:
- Sea L un lenguaje regular, ¿Existe una gramatica lineal por la derecha G que genera L, es decir, L(G)=L, cuyo numero de variables es igual a Indice(RL)? Sí, si una vez que tenemos el AFD mínimo lo transformamos en una gramática lineal por la derecha.
- Si una expresión regular contiene un asterisco (de Kleene) entonces el lenguaje es infinito, ¿Es correcto? Sí, ya que el lenguaje que genera una RegEx sería infinito en el momento que metamos la clausura *.
- Si un autómata determinista mínimo (completo) tiene un solo estado no final (a parte de sus estados finales), entonces dicho estado no final, (si lo dibujamos) tiene una arista reflexiva, ¿es correcto? No, ya que eso depende del proceso de minimización del autómata original.
- Para cada autómata finito con pila no determinista (AFPND) que acepta en estado final, ¿existe un AFPND que acepta con pila vacía? Falso. Un AFPND no tiene otro equivalente: simplemente acepta palabras en su estado final o cuando tiene la pila vacía.
- Dada una gramática lineal por la derecha ambigua G, es posible construir una gramática lineal por la derecha no ambigua G’ que genera el mismo lenguaje, es decir, con L(G’)=L(G)? Sí, ya que de una GLD ambigua sacamos un AFD, el cual lo podemos minimizar quitándole la condición de ambigüedad creando una GLD no ambigua y, a partir de esta, podemos generar la GLI no ambigua.